Acrobot

Summary

• The acrobot is a low-dimensional nonlinear dynamical system that can be used to motivate ideas of nonlinear control for more complicated systems.
• Control strategies for both feedback and open-loop trajectory generation are presented with computational results highlighting key points.

Introduction

Let’s start with a picture:

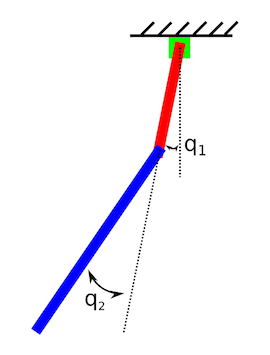
This image represents the physical layout of a pretty cool robotic system known as the acrobot. The system consists of two bars, red and blue, and two joints. One of the two joints is connected to the ceiling, while the other links the two bars. This latter joint is where the fun comes in; this joint is actuated! Ok, ok, maybe it’s not that exciting, but I think that it’s pretty cool. Being able to control the angle $q_2$ from the picture directly will allow us to do some pretty neat things later; like making the acrobot point up against gravity or catch a thrown ball. More on this later.

Why study the acrobot?

So many reasons…

• The acrobot is complex enough to exhibit chaotic behavior while not being so complex as to be mathematically intractable.
• Like many complex robots, the acrobot is underactuated, meaning that it is impossible to make it follow any arbitrary trajectory.
• Controlling the acrobot provides a great introduction to methods of control for more complex systems.

Motivation

I’ll only touch on some key points here; for a more complete treatment, see Sprong or Tedrake.

The acrobot’s state \(\mathbf{x}\) at any given time is described by the following vector:

\[\mathbf{x} = \begin{pmatrix} q_1 \\ q_2 \\ \dot q_1 \\ \dot q_2 \end{pmatrix},\]

and the control input is $u = \ddot q_2$; the actuator can directly change the angular acceleration of $q_2$ only.

I will try and achieve two goals with the acrobot in this post:

• Make the acrobot stand up, meaning balancing the acrobot upright.
• Make the acrobot catch a thrown ball.

The second bullet will follow partially as a consequence of work towards achieving the first. To actually make the acrobot balance requires a few different controllers as it turns out. To motivate why, let’s start by considering how the acrobot moves when the control strategy is poor. Below you’ll find a link to a video showing a really rough and poorly actuated trajectory of the acrobot trying to stand up.

This behavior is suboptimal to be sure, so let’s go through how we might make it better.

Control

LQR

Personally, I like to start controlling nonlinear systems near equilibria. Dealing with minor disturbances once I’ve gotten there is easy: just use LQR. LQR is an optimal control law, meaning that given a desired objective, usually minimizing cost given a set of simplifying assumptions, it’s the best control law we can construct. The desired objective is usually minimizing error between current and desired states.

State evolution using LQR is written as

\[\mathbf{x}_k \approx A (\mathbf{x}_{k-1} - \mathbf{x}_d) + B u,\]

where

• \(\mathbf{x}_k\) is the state vector at time \(k\)
• \(A\) is the state Jacobian matrix
• \(\mathbf{x}_d\) is the desired state vector
• \(B\) is the control Jacobian matrix

The control law for LQR is derived as

\[u = -K (\mathbf{x}-\mathbf{x}_d),\]

where $K$ is the optimal gain discussed in the first section here.

LQR is great, but only when the dynamics of the acrobot are mostly linear, and this assumption is valid near equilibria only. What about away from equilibria?

Partial feedback linearization

Sprong developed a technique for underactuated robotic control that could partially linearize the system. I’ll only state the control law here, but you should check this out for more details if you’re interested. The basic idea stems from the fact that fully actuated robots are feedback linearizable, whereas underactuated robots are not. Partial feedback linearization seeks to simplify the underactuated system as much as possible given the number of controllable degrees of freedom.

We will start with the acrobot manipulator dynamic equations:

\[\ddot q_2 = H^{-1} (Bu - C) \\ B = \begin{pmatrix} 0 \\ 1 \end{pmatrix}, C = \begin{pmatrix} C_1 \\ C_2 \end{pmatrix}, H^{-1} = \begin{pmatrix} a_1 & a_2 \\ a_2 & a_3 \end{pmatrix}.\]

The constants \(C_1, C_2, a_1, a_2, a_3\) are all system-specific and don’t matter much for our general discussion of the method. Now, the gist of partial feedback linearization is that we want a control law such that \(\ddot q_2 = y\), but what should \(y\) be? I’d argue that \(y\) should be something of the form \(y = k_1 q_2 + k_2 \dot q_2\), for some fixed negative gains \(k_1, k_2\). Why does this make sense? The negative feedback acts to oppose large rate change. This is definitely not a rigorous argument, this is a blog post after all . However, in the results that will be presented, the controller works pretty well. The partial feedback linearization control law is written out explicitly as:

\[u = \frac{1}{a_3}(y + a_2 C_1) + C_2.\]

Energy shaping

This is arguably the most ad hoc controller that will be presented, but it works. In fact, it works pretty darned well; even far from equilibrium. The total energy of any physical system, which includes the acrobot, is the sum of the potential, \(V\), and kinetic, \(T\), energies: \(E = T + V\). It would be desirable to construct a feedback control that sought out a desired energy, i.e. the potential energy an equilibrium point. Such a control law exists, and it’s construction is known as energy shaping. The law is written out as:

\[u = k(E_d - E)\dot q_2,\]

where \(E_d\) is the system’s energy at the desired position in state space. For details of this control law, see Tedrake, Section 3.5.

Trajectory Planning

Trajectory planning is super cool, and I’d love to get way into this here, but I don’t want to derail the discussion of the acrobot. I’ll write more on trajectory planning methods in future posts, so fret not.

What is trajectory planning?

If the dynamics of the system are well known, there are a number of analytical tools that can be brought to bear in executing desired movements. Specifically, we can construct a control sequence that optimizes system response. In this context, I’d say that optimizes system response means minimizes control effort, but you can create your own cost function to suit your problem.

The results presented in this post utilize a method known as direct collocation. We break up a starting trajectory into points along that trajectory. These points are called knots. The trajectories between knots are modeled as polynomials of the form:

\[\mathbf{q}_{i}(t) = b_0 + b_1 (t-t_i) + b_2 (t-t_i)^2 \dots + u_i\]

with coefficients \(b_i\) chosen such that the polynomials are \(C^1\) continuous at the knot points. \(C^1\) continuity means continuous with continuous first derivative. The problem then becomes how do we construct a sequence of controls \(\{u_1, u_2, \cdots\}\) at the knot points that matches the system dynamics and is optimal with respect to a desired cost function? We can do so relatively simply, it turns out, with CONSTRAINED OPTIMIZATION!! The constrained optimization problem to be solved can be stated explicitly as:

Assuming a piecewise polynomial representation of \(\mathbf{q}(t)\), find the control sequence \(\{u_1, u_2, \cdots\}\) at knots \(\{ \mathbf{q}_1, \mathbf{q}_2, \cdots \}\) constrained by the given system’s dynamics that minimizes overall cost, which can be represented as a function: \(C( \{\mathbf{q}_i\}, \{u_i\})\).

Typical costs are:

• Minimize control effort: like minimizing fuel consumption of a spacecraft.
• Minimize path length in state space: like a line integral along a trajectory
• Minimize jerk: if there are desired comfort constraints, you can construct a control sequence to avoid excessive jostling

Why trajectory planning?

Well, it’s totally awesome for one thing; breaking down complicated control problems into simpler subproblems and letting a computer crunch out an optimal solution is a nice merging of physics and computation. Personally, I like that it’s a way of exploiting prior system knowledge to construct a controller that utilizes more than current state feedback.

I’ll do more posts on trajectory planning in the future, so stay tuned.

Results

I’ll now go through some results that I generated using CSAIL’s Drake API. This is a nice package for investigating control of real nonlinear dynamical systems. It’s well documented for the most part and it does a lot of cool things out of the box. Like all niche software, though, be prepared to put in some serious effort learning the API.

Standing up

The first question I’ll address is: How can I make the acrobot stand upright? From basic systems theory, we know that the acrobot has two equilibria: a stable point with \(q_1=q_2=0, \dot q_1=\dot q_2 = 0\) and an unstable point with \(q_1=\pi, q_2=0, \dot q_1=\dot q_2 = 0\). The stable equilibrium is so because the system has lowest possible energy, whereas the unstable equilibrium has higher potential energy. Standing the acrobot up is challenging because any kind of unaccounted-for disturbance about the upright equilibrium will allow gravity to pull the system downward towards the stable equilibrium.

Let’s start with the video link presented earlier; the one showing how chaotic the system can be with improperly applied feedback control:

Clearly, there’s some work to be done here. The system response is erratic and hints at the presence of low-dimensional chaos, specifically:

• lack of periodicity
• irregular speedup/slowdown

If we start far from the equilibrium, I suspect that LQR won’t be very effective, so I’ll look at using the other two controllers first; maybe they will be enough. The video link below shows results using partial feedback linearization and energy shaping control:

Ok, these controllers get us close to the goal. Once there, though, the controllers don’t have fine enough resolution to keep the system there indefinitely. I’ll bet LQR could be applied exclusively once we get close enough to the equilibrium. I’ve added a condition to the controller to only use LQR once the cost-to-go has gotten sufficiently small. Results utilizing this new controller applied to the original problem are linked below:

Whoa! Much better! The controller actually stabilizes the acrobot about the desired point, and quickly so. The big takeaways here are:

• Energy shaping and PFL controllers are useful for points far from the upright equilibrium
• LQR is useful for disturbance rejection near the upright equilibrium.

Catching a thrown ball

Now, for something more challenging: Can we get the acrobot to catch something? There are a lot of implementation details here that I won’t discuss; such as creating the system Jacobian matrix, objective construction, etc… I only aim to show that Drake can be used to construct a trajectory for catching a ball with well-known, and perturbed, system dynamics. The basic idea here is that direct collocation is used for generating an optimal control sequence for catching the ball with the acrobot.

First, the easiest case; assume we have perfect state information. See the video link below:

Nice; the acrobot wiggles about and catches the ball at the end of the second bar. Now would be a natural point to discuss trajectory planning in general. The trajectory shown above was planned using perfect information, i.e. it is open-loop. In the real-world, we can typically compile pretty good, though imperfect, information. How well does the planned trajectory do if we perturb the system? At this point, we have pretty good state information; but how sensitive is our solution to small changes?

I guess the answer to the previous question is: pretty darned sensitive! Perhaps there is a way to stabilize our open-loop solution with feedback control. What I’m thinking is that our open-loop trajectory is kind of like a stable structure in our problem space, and perturbing this would result in something that might lie along a mostly-linear extension of that stable structure. So, perhaps, we could implement an LQR controller that would keep the dynamics of the perturbed system in the linear regime allowing us to account for perturbations to the original open-loop trajectory. Let’s see if such a solution would work:

Cool! It worked!

Conclusion

I’ve presented a lot of content with little technical detail. I encourage you to comment with kudos and suggestions for content improvement. I’ve tried to link to sources that provide clarification and deeper exploration of the content presented within this post, but if anything is lacking please say so. I really like working with the acrobot; I think it’s a cool system for presenting ideas to try for more complicated systems. Thanks for reading!