Smooth Path Planning - just the path for now
Motivation
In mobile robot trajectory planning, there are many methods for creating trajectories that guide a robot through a series of waypoints with a desired orientation at each; Bezier splines are one such popular method because they are
- easy to implement with low computational complexity
- geometrically-continuous to arbitrary order, but with added complexity
However, these methods typically come with many design considerations; chiefly among them is the question: How smooth do trajectories need to be for a robot to effectively track them?
I am not trying to answer this question here, since the question is predominantly one that requires a more subtle analysis of the actual robot and its mission in order to provide a satisfactory, rigorous answer. Rather, I will present one method that I have found interesting in my studies: \(\eta^3-\)splines.
What is an $\eta^3-$spline?
An $\eta^3$-spline is a primitive trajectory segment characterized by a shaping parameter, $\eta$, and an order, 3 in this case, which, when stitched together with other like-splines, can be made to form a continuous trajectory. Splines come in all shapes and sizes, each having its own properties; desirable or not.
What makes $\eta^3$-splines so special? They have been proven mathematically to have some very nice properties for mobile robot trajectory planning, particularly wheeled mobile robot planning:
- Trajectories are smooth up to the first-derivative of the curvature. This is desirable because the first-derivative of the curvature being continuous implies that the angular velocity, a.k.a. the torsion, along the path will also be continuous. From a tracking perspective, this is a big win.
- They are the minimal such polynomial spline to achieve the above. Mathematically, there is no lower-order polynomial that can do it.
- The shaping parameter $\eta$ can be chosen arbitrarily to achieve a desired shaping. This can be particularly useful for moving through structured environments with known obstacles or for achieving some other design objective. The following two charts show how changing $\eta$ can reshape splines from the same starting point to the same final point:

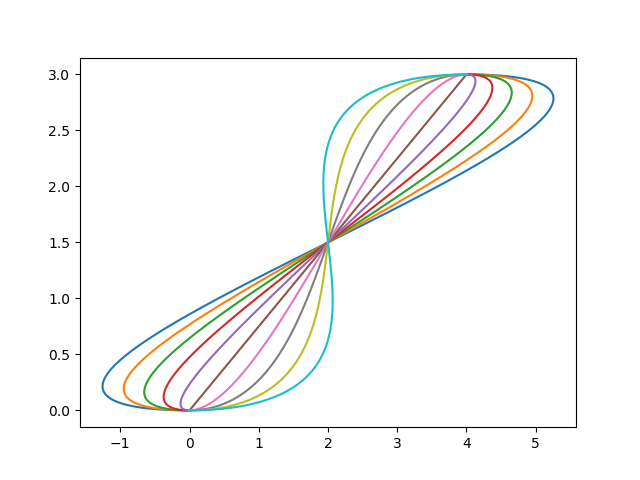
The final point, I believe, I the most useful:
- $\eta^3-$ splines generate, or can be made to closely approximate, many other primitive arcs/spirals/clothoids/etc… This is nice because each of these primitive segments have their own disparate mathematical models that would require separate implementations to use side-by-side. The combination of these multiple primitive segments/splines can be seen in the figure below:
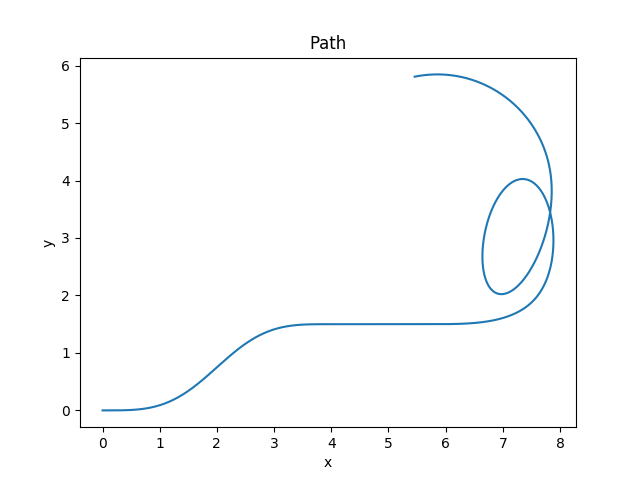
You can check out this repo for the python implementation used to generate the figures above.
We have the path, now what?
This is a good question. We have a smooth path now that has some desirable mathematical properties, but I have not yet mentioned anything about actually moving along the path with a prescribed motion profile. In a future post, I will do just that. For now, I just wanted to present the preliminary work I did to generate the charts included in this post. The trajectory problem is a very interesting one, and I look forward to presenting that work in the near future.