Point Cloud Registration as Optimization, Part One
In this post, I want to talk about how, mathematically, one can formulate point cloud registration as an optimization problem. Point cloud registration is used for egomotion estimation, 3d object tracking, and more.
What is point cloud registration? Let’s start with a motivating picture:
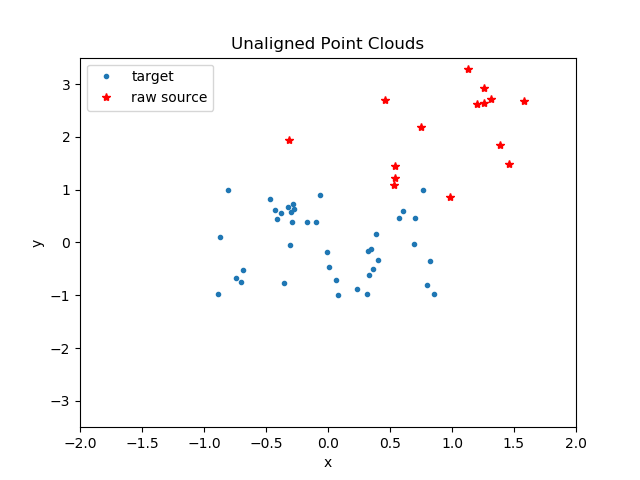
Here, the reader will see two sets of points, otherwise called clouds. As displayed, it is not immediately clear that there is any similarity between the two point clouds, at all. However, if we apply a particular homogeneous transformation to the "source" cloud, we get the following:
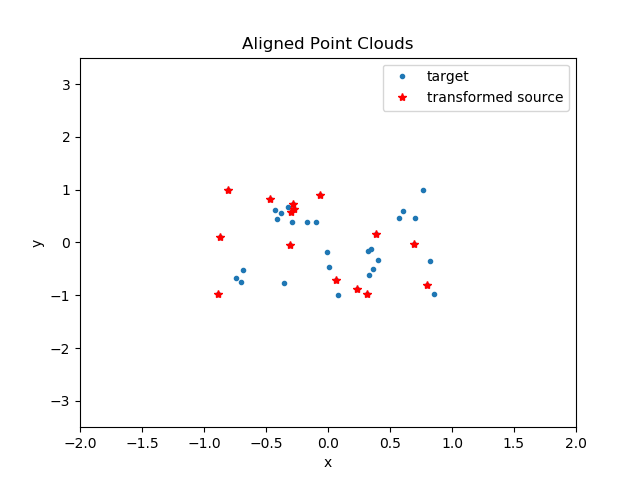
So, the "source" distribution is related to the "target" distribution by a homogeneous transformation; after applying this transformation, the registration error is 0. Why is this useful? Well, if we have prior knowledge of the sensor state before observing the two point distributions, we could use this information to determine motion of the sensor and/or an object in between observations. This information would be very useful in estimating sensor pose or tracking an object.
The million-dollar question then becomes:
How do we find the homogeneous transformation that best aligns the two point clouds?
This question really requires the solution of two problems:
- Find the best set of correspondences between the source and target point clouds
- Using that set of correspondences, find the optimal homogeneous transformation
In this post, I discuss how to formulate the first problem mathematically.
What is a "correspondence"?
A correspondence is a way of defining similarity between points taken from two distinct point clouds: the so-called source and target clouds. "Similarity", in this sense, means invariance of the set pairwise distances between a Point A, from the source cloud, and other points in the source cloud when compared with a corresponding Point B, from the target cloud, and a subset of other points in the target cloud.
I have added the caveat "a subset" because, in practice, it is assumed that the number of source points, \(m\), is less than the number of target points, \(n\). This is to allow for more robust matching.
Finding optimal correspondences
Now, onto the crux of the matter: How to find the best correspondences?
Let’s start by defining a discrete state-space for matches, \(X = \{0, 1\}^{mn}\), where \(\mathbf{x} \in X\) can be represented as:
\[x_{in+j} = \begin{cases} 0 & \text{point $i$ does not match point $j$} \\ 1 & \text{point $i$ matches point $j$} \end{cases},\]\(i\) is a point in the source cloud, \(j\) is a point in the target cloud, \(m\) is the number of source points, and \(n\) is the number of target points. \(m < n\), by assumption, avoids overconstraining the matching problem.
The “best correspondences” problem can be formulated as an optimization problem:
Find the vector \(\mathbf{x}^*\) that maximizes the quadratic objective function: \(\begin{eqnarray} f(\mathbf{x}) = \sum_{ijkl} w_{ijkl} x_{in+j} x_{kn+l} \end{eqnarray}\)
where
\[\begin{eqnarray} w_{ijkl} = \exp{[-d_{ijkl}]} \\ d_{ijkl} = \bigl | ||\mathbf{p}_i - \mathbf{p}_k||_2 - ||\mathbf{p}_j - \mathbf{p}_l||_2 \bigr |. \end{eqnarray}\]
\(\mathbf{p}_i, \mathbf{p}_k\) are the 3d cartesian coordinates of points \(i\) and \(k\) in the source cloud, whereas \(\mathbf{p}_j, \mathbf{p}_l\) are the 3d cartesian coordinates of points \(j\) and \(l\) in the target cloud.
The \(d\) value above is interpreted as a pairwise consistency metric: the smaller the value of \(d\), the better the correspondence between the pair \((i, k)\) in the source cloud to the pair \((j, l)\) in the target cloud. By adding the \(\exp[\cdot]\) function, stronger correspondences will be weighted exponentially higher than weaker ones, which will favor better matches during the search for the optimal \(\mathbf{x}^*\).
There are some additional factors to consider; namely, what are the constraints on \(\mathbf{x}^*\)? For one, only one source point can be matched to a target point, and vice-versa. Moreover, we want every source point to be matched to a target point. Mathematically, these constraints can be stated as:
\[\begin{eqnarray} \sum_{j=0}^{n-1} x_{in+j} = 1 \ \ \forall i \in [0, m)\\ \sum_{j=0}^{n-1} x_{mn+j} = n - m \\ \sum_{i=0}^{m} x_{in+j} = 1 \ \ \forall j \in [0, n) \end{eqnarray}\]where the slack variables \(x_{mn+j}, 0 \le j < n\) are added to address the target points that are not matched to a source point.
Now, we have everything we need to find the optimal \(\mathbf{x}^*\) right? Well, not quite. It turns out that the problem, as presented, is NP-hard! In a future post, I will discuss how to relax the problem presented to make it solvable with a continuous optimization approach.
Once we have the solution to the correspondence problem, we can find the best homogeneous transformation between the source and target point clouds using Kabsch’s algorithm. But, this will come in the next post.
Summary
In this post, I presented point cloud matching as an optimization problem. I developed the mathematical framework needed to describe the problem. I will present a method for solving the relaxed problem in a future post. If you don’t want to wait, you can check out the working repo here.
Thanks for reading!