Finding Point Cloud Correspondences Using Undirected Graphs
In this post, I will discuss an alternate approach to the point cloud correspondences problem using graph-based methods. This post is meant to be interactive and those who wish to run the code for yourselves, check out the jupyter notebook from which this post was derived.
Let’s start with some dependencies:
import numpy as np
import matplotlib.pyplot as plt
from copy import deepcopy
import time
I want to create a set of points randomly sampled from a square. These points will be used as the basis for subsequent demos. First, let’s set the random seed for repeatability of experiments.
np.random.seed(seed=11011)
To setup the data for the experiments, we will define values for the following parameters:
-
mis number of points in source cloud -
nis number of points in target cloud -
noise_valis the 1-sigma value for applying noise (per channel $x,y$) -
angis the rotation angle (ccw is positive) to apply -
xtis the $x$ translation to apply -
ytis the $y$ translation to apply
m, n = 15, 25
noise_val = 0.
ang = np.pi / 4.
xt, yt = 10.0, 15.0
side_length = 20
Let’s sample some points and apply a transformation to get two point sets for comparison:
# uniformly sample on square with dimensions side_length x side_length
# use homogeneous coordinates
target_pts = side_length * np.random.random((4, n)) - 0.5 * side_length
target_pts[2, :] = 0.
target_pts[3, :] = 1.
# transform
ca, sa = np.cos(ang), np.sin(ang)
tgt_to_src = np.array([[ca, sa, 0., xt],
[-sa, ca, 0., yt],
[0., 0., 1., 0.],
[0., 0, 0., 1.]])
target_pts_xform = np.dot(tgt_to_src, target_pts)
correspondences = np.random.choice(n, m, replace=False)
# subsample and reorder target points
source_pts = target_pts_xform[:, correspondences] + noise_val*np.random.randn(4, m)
source_pts[2, :] = 0.
source_pts[3, :] = 1.
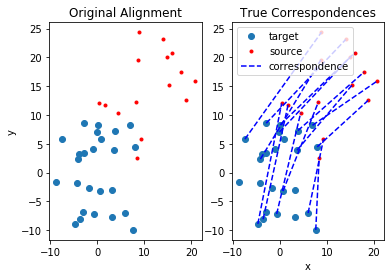
Recall: A correspondence is encoded by two points: one from the source point cloud and the other from the target point cloud. Such correspondences can be encoded as vertices in an undirected graph enumerated as $i’ \equiv i n + j$, with source point $i$ and corresponding target point $j$. For more details, check out the following paper. For comparison of methods below, let’s start by identifying the true correspondences between the source and target point sets and plot the data:
correspondenceVertices = [] # for comparison below
for i,c in enumerate(correspondences):
correspondenceVertices.append(i*n + c)
print("Correspondence vertices list is {}".format(correspondenceVertices))
Correspondence vertices list is [23, 41, 72, 88, 105, 137, 165, 189, 219, 234, 267, 283, 301, 328, 374]
plt.figure()
ax1 = plt.subplot(121)
ax1.plot(target_pts[0, :], target_pts[1, :], 'o', source_pts[0, :], source_pts[1, :], 'r.')
ax1.set_ylabel("y")
ax1.set_title("Original Alignment")
ax2 = plt.subplot(122)
ax2.plot(target_pts[0, :], target_pts[1, :], 'o', label="target")
ax2.plot(source_pts[0, :], source_pts[1, :], 'r.', label="source")
legend_made = False
for i, c in enumerate(correspondences):
if not legend_made:
ax2.plot([target_pts[0, c], source_pts[0, i]], [target_pts[1, c], source_pts[1, i]], 'b--', label="correspondence")
legend_made = True
else:
ax2.plot([target_pts[0, c], source_pts[0, i]], [target_pts[1, c], source_pts[1, i]], 'b--')
ax2.legend()
ax2.set_title("True Correspondences")
ax2.set_xlabel("x")
plt.show()
You’re probably asking at this point: How do we go about actually finding the true correspondences? We need the notion of pairwise consistency:
Two correspondences are pairwise consistent iff:
- The source points from each correspondence are a minimum of
pairwiseThresholddistance apart; call this distanced1 - The target points from each correspondence are a minimum of
pairwiseThresholddistance apart; call this distanced2 - The absolute value of the difference between
d1andd2is at maximumepsilondistance apart.
for some epsilon, d1, and d2 greater than 0. This provides a significant restriction/constraint for our problem, as it allows us to discard unreasonable correspondence edges based on a simple consistency check based on distance.
We can create a pairwise-consistency check as follows:
def isPairwiseConsistent(ci, cj, epsilon=0.1, pwThresh=0.1):
# ci - i*n + i', i \in source, i' \in target
# cj - j*n + j', j \in source, j' \in target
# ci.x is 3x1 numpy array
# ci.y is 3x1 numpy array
# cj.x is 3x1 numpy array
# cj.y is 3x1 numpy array
d1 = np.linalg.norm(ci["x"] - cj["x"])
d2 = np.linalg.norm(ci["y"] - cj["y"])
d3 = np.abs(d1 - d2)
return d1 >= pwThresh \
and d2 >= pwThresh \
and d3 <= epsilon
isPairwiseConsistent returns true when two correspondences, ci and cj, are pairwise consistent. isPairwiseConsistent returning True means that we need to create and edge between the two input correspondence vertices. The graph structure should now be becoming clear in your mind: possible correspondences are encoded as vertices of an undirected graph with edges between correspondences determined by the pairwise consistency check. To find the best possible set of correspondences, we can compute the maximum clique of the graph, which represents the subgraph of largest size where all correspondence vertices are pairwise consistent with each other (i.e. have edges connecting each correspondence to every other correspondence in the subgraph).
Before getting to a couple of approaches for computing the maximum clique, I’ll define a few helper functions for comparison of algorithm output to ground truth
def cliquesAreEquivalent(cliqueOne, cliqueTwo):
return cliqueOne.sort() == cliqueTwo.sort()
User-defined constants:
-
epsilonabove $\to$eps -
pairwiseThresholdabove $\to$pwThr
eps = 1e-1
pwThr = 1e-1
Construct vertices and edges for maximum clique calculation.
E = []
V = []
for i in range(source_pts.shape[1]):
for j in range(target_pts.shape[1]):
for k in range(source_pts.shape[1]):
for l in range(target_pts.shape[1]):
if i != k and j != l:
ci = {"x": source_pts[:3, i], "y": target_pts[:3, j]}
cj = {"x": source_pts[:3, k], "y": target_pts[:3, l]}
consis = isPairwiseConsistent(ci, cj, epsilon = eps, pwThresh = pwThr)
if consis:
V1 = i*n + j
V2 = k*n + l
E.append((V1, V2))
if V1 not in V:
V.append(V1)
if V2 not in V:
V.append(V2)
Python has a useful library for graph processing called networkx. As a baseline, let’s setup a workflow using networkx to compute the maximum clique.
Maximum Clique Identification using networkx
import networkx as nx
G = nx.Graph()
G.add_edges_from(E)
cliques = list(nx.find_cliques_recursive(G))
#plt.figure()
#nx.draw(G, with_labels=True)
maxClique = []
maxCliqueSize = 0
tBegin = time.time()
for c in cliques:
if len(c) > maxCliqueSize:
maxClique = c
maxCliqueSize = len(c)
timeElapsed = time.time() - tBegin
print("Max clique was found in {}sec".format(timeElapsed))
print("Max clique has size {}".format(maxCliqueSize))
print("Max clique is {}".format(maxClique))
Max clique was found in 0.000392913818359375sec
Max clique has size 15
Max clique is [105, 234, 165, 72, 328, 41, 137, 267, 301, 219, 374, 88, 283, 189, 23]
Check that maxClique is equivalent to the true correspondences.
print("Is the correspondence list equivalent to the max clique? {}".format(cliquesAreEquivalent(correspondenceVertices, maxClique)))
Is the correspondence list equivalent to the max clique? True
The approach above shows that the max clique of the graph does, indeed, identify the true correspondences. The approach above is useful if you are developing under a native Python environment. Unfortunately, no equivalent library for C++ is available. We can use branch-and-bound based algorithms for computing the max cliques in a purely algorithmic way; such approaches can be implemented easily in other languages.
Practical Maximum Clique Algorithms
The first two max clique algorithms from here are implemented below. First, let’s define a few routines for computing needed quantities
def adjacency(edges, vertex):
adj = []
for e in edges:
if vertex in e:
adj.append(e[0]) if vertex != e[0] else adj.append(e[1])
return adj
As a quick check, reproduce the simple example from the paper:
# unit test for adjacency using graph from paper (Figure 2)
V = [1, 2, 3, 4, 5, 6]
E = [(1, 2), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 6)]
for v in V:
print("v: {}, adj(V): {}".format(v, adjacency(E, v)))
v: 1, adj(V): [2, 5, 6]
v: 2, adj(V): [1, 3, 4, 5]
v: 3, adj(V): [2, 4, 5]
v: 4, adj(V): [2, 3, 5]
v: 5, adj(V): [1, 2, 3, 4, 6]
v: 6, adj(V): [1, 5]
Basic BnB (Algorithm 1)
def mcBasicBnB(S, edges):
global R, Rbest
"""
Algorithm 1 from paper "A Practical Maximal Clique for Matching with Pairwise Constraints" by
Bustos et.al
args:
S - candidate vertices for expansion
edges - edges of (undirected) graph
"""
while S:
if len(R) + len(S) <= len(Rbest):
return
v = S[0]
R.append(v)
Sprime = [vert for vert in S if vert in adjacency(edges, v)]
if Sprime:
mcBasicBnB(Sprime, edges)
elif len(R) > len(Rbest):
Rbest = deepcopy(R)
R.remove(v)
S.remove(v)
R, Rbest = [], []
V = [1, 2, 3, 4, 5, 6]
E = [(1, 2), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 6)]
mcBasicBnB(V, E)
print("Rbest is: {}".format(Rbest))
Rbest is: [2, 3, 4, 5]
Which matches the article’s result.
Quick check: Does mcqBasicBnB find the correspondences like the previous method tried (i.e. the one using networkx )?
E = []
V = []
for i in range(source_pts.shape[1]):
for j in range(target_pts.shape[1]):
for k in range(source_pts.shape[1]):
for l in range(target_pts.shape[1]):
if i != k and j != l:
ci = {"x": source_pts[:3, i], "y": target_pts[:3, j]}
cj = {"x": source_pts[:3, k], "y": target_pts[:3, l]}
consis = isPairwiseConsistent(ci, cj, epsilon = eps, pwThresh = pwThr)
if consis:
V1 = i*n + j
V2 = k*n + l
E.append((V1, V2))
if V1 not in V:
V.append(V1)
if V2 not in V:
V.append(V2)
R, Rbest = [], []
tBegin = time.time()
mcBasicBnB(V, E)
timeElapsed = time.time() - tBegin
print("Max clique was found in {}sec".format(timeElapsed))
maxCliqueBasicBnB = deepcopy(Rbest)
print("Is the correspondence list equivalent to the mcBasicBnB maximum clique? {}".format(cliquesAreEquivalent(correspondenceVertices, maxCliqueBasicBnB)))
Max clique was found in 4.391311883926392sec
Is the correspondence list equivalent to the mcBasicBnB maximum clique? True
Cool. maxCliqueBasicBnB works but is pretty slow (though it is faster than the quadratic assignment approach. Let’s try Algorithm 2.
MCQ (Algorithm 2)
def first_available(colors):
"""Return smallest integer not in the given list of colors."""
count = [0] * (len(colors) + 1) # Allocate long-enough array of zeros
for color in colors:
if color < len(count):
count[color] += 1
for color in range(len(colors) + 1):
if count[color] == 0:
return color
def greedy_color(vertices, edges):
"""Find the greedy coloring of graph defined by edges in the given vertices.
"""
color = dict()
for v in vertices:
color[v] = first_available([color[w] for w in adjacency(edges, v) if w in color])
for key in color:
color[key] += 1 # make sure to start coloring from 1
return color
def mcMCQ(S, edges, f):
global R, Rbest
"""
Algorithm 2 from paper "A Practical Maximal Clique for Matching with Pairwise Constraints" by
Bustos et.al
args:
S - candidate vertices for expansion
edges - edges of (undirected) graph
f - coloring of vertices for expansion (len(f) == len(S), by necessity)
"""
# reorder vertices in S by adjacency
#Ssrt = sorted(S, key=lambda x: len(adjacency(edges, x)), reverse=True) # this does not work
Ssrt = sorted(S, key=lambda x: len(adjacency(edges, x)), reverse=False) # this works, want to expand about vertex of largest degree first
#Ssrt = S # this also works
while Ssrt:
v = Ssrt[-1]
if len(R) + f[v] <= len(Rbest):
return
R.append(v)
Sprime = [vert for vert in Ssrt if vert in adjacency(edges, v)]
if Sprime:
fprime = greedy_color(Sprime, edges)
mcMCQ(Sprime, edges, fprime)
elif len(R) > len(Rbest):
Rbest = deepcopy(R)
R.remove(v)
Ssrt.remove(v)
R, Rbest = [], []
V = [1, 2, 3, 4, 5, 6]
E = [(1, 2), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 6)]
f = greedy_color(V, E)
#print(f)
mcMCQ(V, E, f)
print("Rbest is: {}".format(Rbest))
Rbest is: [5, 2, 4, 3]
E = []
V = []
for i in range(source_pts.shape[1]):
for j in range(target_pts.shape[1]):
for k in range(source_pts.shape[1]):
for l in range(target_pts.shape[1]):
if i != k and j != l:
ci = {"x": source_pts[:3, i], "y": target_pts[:3, j]}
cj = {"x": source_pts[:3, k], "y": target_pts[:3, l]}
consis = isPairwiseConsistent(ci, cj, epsilon = eps, pwThresh = pwThr)
if consis:
V1 = i*n + j
V2 = k*n + l
E.append((V1, V2))
if V1 not in V:
V.append(V1)
if V2 not in V:
V.append(V2)
R, Rbest = [], []
f = greedy_color(V, E)
tBegin = time.time()
mcMCQ(V, E, f)
timeElapsed = time.time() - tBegin
maxCliqueMCQ = deepcopy(Rbest)
print("Max clique was found in {}sec".format(timeElapsed))
print("Is the correspondence list equivalent to the mcMCQ maximum clique? {}".format(cliquesAreEquivalent(correspondenceVertices, maxCliqueBasicBnB)))
Max clique was found in 0.07146430015563965sec
Is the correspondence list equivalent to the mcMCQ maximum clique? True
This algorithm is significantly faster than the basic BnB with the same result. You should take care to analyze runtime performance for your particular m, n: for smaller m, n, you should use the basic BnB.
Conclusion
The work described in this post was used as the basis for the mc algorithm in my project nmsac. The graph-based methods provide a faster, simpler way of identifying point-to-point correspondences between two point clouds. I wanted to write up this post as a primer similar to the posts done for the qap algorithm, which solves the correspondence problem using optimization-based methods. This is the last post relating to nmsac before the final project write-up, which should be completed in the next few weeks.
Thanks for reading!